Vocal-Tract Simulation
Time-domain acoustic simulation of VT with side-branches

By mathematically reformulating Maeda's famous 1-D time-domain model of vocal-tract acoustics, we extended it to allow any number of internal side-branches such as the bilateral piriform fossae, thus enabling more natural-sounding articulatory synthesis of speech.


BACKGROUND Algorithms for computer simulation of vocal-tract acoustics can be categorized broadly as either frequency- or time-domain. One of the most well known and widely used of the time-domain methods, is the one elaborated by Shinji Maeda (Speech Communication, 1982), which in turn was derived from the earlier work of James Flanagan and colleagues (Bell Systems Tech. J., 1975). Time-domain acoustic modeling of the vocal-tract has the advantage of dealing more naturally with transient sounds such as consonants, as well as accounting more naturally for acoustic interactions between vocal-fold and vocal-tract airflows.

However, time-domain models were limited to modeling the vocal-tract main airway (from glottis to lips) and only one side-branch (usually the nasal tract). On the other hand, increasing evidence points to the acoustic importance of vocal-tract side-branches such as the piriform fossae (which extend bilaterally from the main airway in the hypopharynx): it is increasingly believed that such detailed geometries potentially lend naturalness and individuality to a person's voice. In this project, we therefore aimed to overcome the one side-branch limitation, by examining in detail Maeda's time-domain model and rederiving its mathematical formulation to allow any number of side-branches.

VT Transmission Line with Side-Branches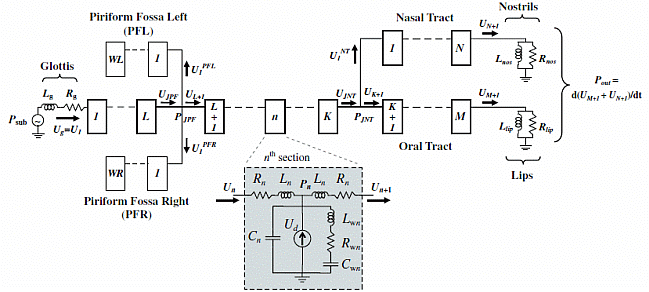

SINGLE-MATRIX FORMULATION The basis of the established time-domain vocal-tract model is discretization in space and time, of the three partial differential equations that describe acoustic wave propagation in a tube with non-rigid walls (the equations of momentum, continuity, and wall-vibration). This leads to an equivalent representation of the vocal-tract in terms of an electrical lumped transmission-line (as shown above), with each T-section representing the length, cross-sectional area, and perimeter of its physical counterpart.

Maeda (1982) used the trapezoid rule for time discretization, and rearranged the transmission-line equations into 3 sets of linear algebraic equations, that were ultimately expressed as 3 matrix equations involving mainly volume-velocities: one set for the sections from glottis up to the nasal-tract junction, a second set for the sections from that junction to the lips, and a third set for the sections from the junction to the nostrils. Thus in the original formulation, the simulator was hard-wired to deal with only one side-branch: that of the nasal tract, attached to the main tract at a particular junction corresponding physically to the velar opening.

As detailed in Mokhtari (2006) and in Mokhtari et al. (2008), we generalized the algorithm to any desired number of side-branches, by reformulating the sets of equations into a single matrix equation. As shown above, our specific example retained the nasal tract while adding two additional side-branches: the left and right piriform fossae. A comparison of vocal-tract transfer functions calculated by the new model for five vowels revealed a good match with transfer functions calculated by an equivalent frequency-domain model.

Our single-matrix formulation of the time-domain model thus proved to be accurate in terms of the expected spectral peaks (poles) and dips (zeros) of steady-state vocalic configurations, while also promising all the transient- and dynamics-related advantages of time-domain models in general. Indeed, based on this work we also proposed a time-domain speech synthesis system based on MRI-measured vocal-tract geometries (Kitamura et al., 2006).

IMPACT It gives us great pleasure to know that the single-matrix formulation has sparked renewed interest and prompted further developments:
  • Ho et al. (2011) extended the computational model to include the branching structure of the tracheobronchial airways below the glottis, and also coupled the model with the classical, self-oscillating two-mass vocal fold model.

  • Elie & Laprie (2016) extended the computational model to include the possibility of bilateral channels within the main vocal-tract (as occur during production of lateral consonants), and also connected a self-oscillating vocal fold model with a glottal chink.

REFERENCES (chronological) J. L. Flanagan, K. Ishizaka & K. L. Shipley (1975)
Synthesis of speech from a dynamic model of the vocal cords and vocal tract
Bell Systems Technical Journal, 54(3), 485-506.

S. Maeda (1982)
A digital simulation method of the vocal-tract system
Speech Communication, 1(3-4), 199-229.

T. Kitamura, H. Takemoto, P. Mokhtari & T. Hirai (2006)
An MRI-based time-domain speech synthesis system
poster presented at the 4th Joint Meeting of the Acoust. Soc. of America and the Acoust. Soc. of Japan, Hawaii, USA
abstract 1pSC5 in J. Acoust. Soc. Am., 120(5) Pt.2, 3037.

P. Mokhtari (2006)
Direct computational method of including piriform fossae and nasal cavity in a time-domain acoustic model of the vocal tract
poster presented at the 4th Joint Meeting of the Acoust. Soc. of America and the Acoust. Soc. of Japan, Hawaii, USA
abstract 5pSC6 in J. Acoust. Soc. Am., 120(5) Pt.2, 3372.

P. Mokhtari, H. Takemoto & T. Kitamura (2008)
Single-matrix formulation of a time domain acoustic model of the vocal tract with side branches
Speech Communication, 50(3), 179-190.

J. C. Ho, M. Zañartu & G. R. Wodicka (2011)
An anatomically-based, time-domain acoustic model of the subglottal system for speech production
J. Acoust. Soc. Am., 129(3), 1531-1547.

B. Elie & Y. Laprie (2016)
Extension of the single-matrix formulation of the vocal tract: Consideration of bilateral channels and connection of self-oscillating models of the vocal folds with a glottal chink
Speech Communication, 82, 85-96.


Copyright ©Parham Mokhtari 2000-2024 Updated: 08 February 2017