|
3D Acoustics Simulation
For 3D simulation of acoustics with the finite-difference time-domain method, an empirical formula was found for determining the optimum parameters of the outermost, absorbing layers, yielding the highest signal-to-noise ratio. |
| FDTD SIMULATION |
Since its inception by Yee (1966), the finite-difference time-domain (FDTD) method has been widely used for computer simulation of wave propagation and related phenomena, not only in electrodynamics and elastodynamics but also, relatively more recently, in acoustics. In the acoustic FDTD method, a region of interest enveloping one or more scattering objects is represented in a 3D grid, with basic properties assigned to each elemental cell: material density, speed of sound, and an energy loss factor. Simulation is then implemented on a digital computer by numerical solution of the fundamental equations of physical acoustics, discretized in both space and time. |
| ABSORBING BOUNDARIES |
As the entire 3D grid must necessarily be of finite volume to allow implementation on a computer with finite memory storage, the outermost layer(s) of cells must be treated in a special way to avoid artifactual reflections of acoustic waves from the computation domain boundaries. In essence, outgoing waves must appear to be absorbed upon contact with the outermost boundary, regardless of the angle of incidence. Influential work on so-called "absorbing boundary conditions" includes Bérenger's (1994) perfectly matched layer (PML), Chew and Weedon's (1994) reposing of the PML in terms of stretched coordinates, and Liu & Tao's (1997) application of these methods to simulation of acoustics in absorptive media. |
| OPTIMUM PML |
However, for 3D simulation of acoustics, there has not appeared a systematic evaluation nor a specific recommendation as to the optimum value of the loss factor (i.e., the extent of coordinate stretching) within the PML. We therefore carried out simulations of a lossless, homogeneous field, with a point source at its center. Defining the acoustic waves radiating outwards from the point source as the "signal", and any reflections from the PML as artifact or "noise", we evaluated the signal-to-noise ratio (SNR) for both linear and quadratic profiles in the PML loss factor, and as a function of the size of the regular (non-PML) region, the number of PML layers, the grid resolution, and the speed of sound in the medium.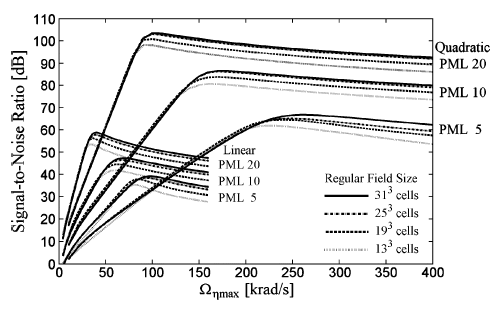
As shown above (Mokhtari et al., 2010), increasing the PML loss factor does not simply increase the signal-to-noise ratio monotonically; instead, SNR reaches an optimum value before succumbing to increased reflections caused by the non-continuous (discrete) nature of the PML. Fortunately, the specific parameter values yielding the peak in SNR in a variety of scenarios could be predicted well by an empirical formula (see Eq.11 in Mokhtari et al., 2010). Thus, for any given grid resolution and speed of sound in the medium, a decision would first be made as to whether a linear or a quadratic PML profile was more appropriate, and how many layers would be necessary to ensure an acceptable SNR (see Fig.2 in Mokhtari et al., 2010), then Eq.11 of Mokhtari et al. (2010) would be used to set the PML loss factor for optimum SNR (i.e., minimum reflections from the domain boundaries). |
| REFERENCES (chronological) |
K. S. Yee (1966) Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media IEEE Transactions on Antennas and Propagation, 14(3), 302-307. J.-P. Bérenger (1994) A perfectly matched layer for the absorption of electromagnetic waves J. Comput. Phys., 114, 185-200. W. C. Chew & W. H. Weedon (1994) A 3D perfectly matched medium from modified Maxwell's equations with stretched coordinates Microw. Opt. Tech. Lett., 7(13), 599-604. Q.-H. Liu & J. Tao (1997) The perfectly matched layer for acoustic waves in absorptive media J. Acoust. Soc. Am., 102(4), 2072-2082. P. Mokhtari, H. Takemoto, R. Nishimura & H. Kato (2010) Optimum loss factor for a perfectly matched layer in finite-difference time-domain acoustic simulation IEEE Trans. on Audio, Speech, and Language Processing, 18(5), 1068-1071. |
| Copyright ©Parham Mokhtari 2000-2024 |
Updated: 25 March 2017 |